Kostprijsberekening en interne informatievoorziening/Break-even

In de eerste berekeningen van de productiviteit van Marcel is aangenomen dat zijn werktempo ongeveer ligt bij het werktempo van Robert. Indien het werktempo van Marcel aanzienlijk lager is dan dat van Robert is er zelfs kans dat de dekkingsbijdrage te laag wordt. Laten we eens rekenen wat er gebeurt als Marcel slechts in staat is om 1 zadelbok per dag te maken.

Een zadelbok per dag betekent dat er slechts 60 zadelbokken in 3 maanden worden geproduceerd. De totale variabele kosten (hout) voor 60 zadelbokken is € 1800 (60 x 30). De totale arbeidskosten (vaste kosten) blijft op € 6.000 en dus worden de totale kosten € 7.800. De opbrengst van 60 zadelbokken is € 6.000 en dus zou een verlies resulteren van € 1800.

Een interessante vraag die we nu gaan bekijken is hoeveel zadelbokken Marcel zou moeten produceren zodat geen winst en geen verlies wordt gemaakt: die wordt break-even genoemd.

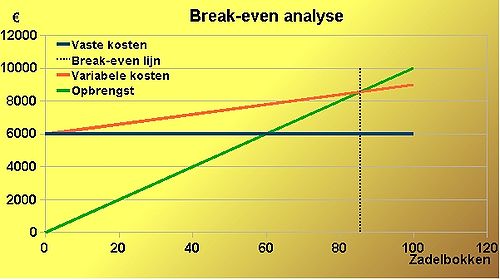
Break-even analyse

Laten we de vraag van deze break-even analyse eens omzetten in een mathematische vergelijking, hoeveel zadelbokken moeten verkocht worden om de totale kosten te dekken:

• X = Aantal zadelbokken
• Vaste kosten = € 6000
• Variabele kosten = € 30 × X
• Opbrengst = € 100 × X

$100\cdot X=6000+30\cdot X$

$(100-30)X=6000$

$X=\frac{6000}{70}=85,7$

De onderneming maakt pas winst als binnen de 3 maanden meer dan 85 zadelbokken worden verkocht en dat komt overeen met een productiviteit van Marcel van 1,42 zadelbokken per dag.

Nog meer kosten, maar ook besparingen - Terug naar dekkingsbijdrage Sjabloon:Sub