Fysica/Kinematica

De kinematica, de bewegingsleer, bestudeert en beschrijft de beweging van lichamen. Het gaat om de plaats en snelheid van het lichaam in ruimte en tijd, en de veranderingen daarin.

Daarbij wordt onderscheid gemaakt in verschillende soorten beweging:

• Eenparige beweging: het lichaam beweegt met constante snelheid
• Eenparig versnelde beweging: het lichaam ondergaat een constante versnelling
• Niet-eenparige beweging: de snelheid verandert, de versnelling is niet constant

De kinematica houdt zich niet bezig met de oorzaak van de beweging, en de veranderingen die in bewegingen kunnen optreden: dat is het terrein van de dynamica.

Eenparige rechtlijnige beweging

De eenvoudigste vorm van beweging is wel de beweging met constante snelheid langs een rechte lijn. Daarbij worden steeds in gelijke perioden gelijke afstanden afgelegd.

Algemeen kunnen we stellen dat een voorwerp in evenwicht is wanneer:

• Het voorwerp niet beweegt.
• Het voorwerp aan alle kanten ondersteund wordt.
• Het voorwerp een eenparige rechtlijnige beweging uitvoert.
• De resulterende kracht op het voorwerp nul is.

afgelegde weg

De beweging kan worden beschreven door de weg s die in de tijd t sinds het begin van de beweging, is afgelegd. De afgelegde weg is een eenvoudige functie van de tijd t:

$s(t)=vt$.

plaats

Ook kan de beweging beschreven worden door de plaats x op de lijn op het tijdstip t. Als de beweging begon in het punt $x_0$, geldt:

$x(t)=x_0+vt$.

verplaatsing

Als een voorwerp zich op een tijdstip t₁ op de plaats x₁ bevindt en op een tijdstip t₂ op de plaats x₂, is de verplaatsing in de tijdsduur $\mathrm{\Delta }t=t_2-t_1$:

$\mathrm{\Delta }x=x_2-x_1$

snelheid

De gemiddelde snelheid v_gem van een object dat over een afstand Δx beweegt gedurende een tijdsduur Δt kunnen we als volgt berekenen:

$v_{gem}=\frac{\mathrm{\Delta }x}{\mathrm{\Delta }t}$

Niet-eenparige rechtlijnige beweging

versnelling

De versnelling a is de verandering van de snelheid van het object over de tijd, en is de afgeleide van de snelheid.

$a(t)=\frac{dv}{dt}$

Indien een voorwerp eenparig rechtlijnig beweegt, is de versnelling gelijk aan nul. Wanneer de versnelling a een constante is ongelijk aan nul, noemen we de beweging een eenparig versnelde rechtlijnige beweging.

Eenparig versnelde rechtlijnige beweging

Indien een voorwerp vanaf plaats x₀ met beginsnelheid v₀ versnelt met een constante versnelling a, is de plaats van het voorwerp als functie van de tijd:

$x(t)=x_0+v_{0}t+\begin{array}{c}\frac{1}{2}\end{array}a{t}^2$

Hierin is:

x0 : de beginpositie (m) v0 : de beginsnelheid (m/s) a : de versnelling (m/s2)

Nu kunnen we de snelheid ook in functie van de snelheid uitdrukken:

$v(t)=v_0+at$

Hierin is:

v0 : de beginsnelheid (m/s) a : de versnelling (m/s2)

Sjabloon:Vragen

Valbeweging

De snelheid van een vallend voorwerp neemt voortdurend toe. Als de snelheid toeneemt spreken we van een versnelling, maar het is moeilijk om die te meten. Het is zelfs moeilijk om de snelheid van een voorwerp op een bepaald moment te meten. Galileï's knikker rolde in de eerste seconde 1 meter. Maar betekent dat dat de knikker een snelheid had van 1 meter per seconde (afgekort 1 m/s)? Nee, niet precies. 1 m/s is alleen maar de gemiddelde snelheid in de eerste seconde. De snelheid verandert voortdurend en dat maakt het zo lastig om hem te meten.

Als je bijvoorbeeld de snelheid van een auto wilt meten, dan kun je dat doen door twee punten te kiezen op de route waar de auto langskomt. Je noteert hoe laat de auto op punt A is en hoe laat hij op punt B is. De gemiddelde snelheid over dat traject is de afstand tussen de twee punten, gedeeld door de tijd die de auto er over doet. Maar we willen geen gemiddelde snelheid weten! We willen precies weten, hoe snel de auto reed om half twee 's middags. En dat is niet op deze manier te meten! We meten altijd het gemiddelde over een traject, nooit de snelheid op een bepaald moment.

Galileï zag dit wel in, maar hij kon het probleem niet oplossen. Newton loste het wel op en daarmee droeg hij niet alleen bij aan onze kennis over de natuurkunde, maar ook aan die over de wiskunde!

Afgelegde weg van een knikker, 1 meting per seconde

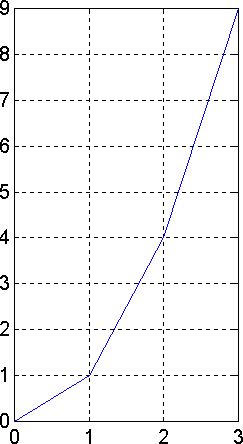
Hier zie je de meetresultaten van Galileï in een grafiek uitgezet. Horizontaal is de tijd uitgezet en verticaal de totale afgelegde afstand. Je ziet dat de grafiek elke seconde een knik heeft. Zo is het in werkelijkheid natuurlijk niet, de snelheid van de knikker verandert de hele tijd, niet 1x per seconde. Dat het er zo uit ziet, komt alleen doordat we maar een paar meetpunten hebben en die met rechte lijnen met elkaar hebben verbonden.

De helling (of "Richtingscoëfficiënt") van de lijnstukken komt overeen met de gemiddelde snelheid van de knikker op dat stuk van het traject. Tussen t=0 en t=1 is de gemiddelde snelheid 1 m/s en de lijn heeft een richtingscoëfficiënt van 1. Tussen t=1 en t=2 is de gemiddelde snelheid 3 m/s en de richtingscoëfficiënt is 3. Tussen t=2 en t=3 zijn ze beide gelijk aan 5 enzovoort. Dat zijn dus inderdaad die opeenvolgende oneven getallen, die Galileï had ontdekt.

Maar je kunt aan de knikken duidelijk zien, dat deze lijn geen goede weergave is, van wat er in werkelijkheid gebeurt.

Afgelegde weg van een knikker, 2 metingen per seconde

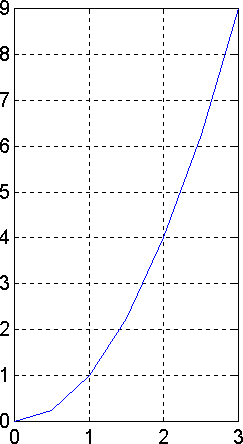
Als we meer meetpunten gebruiken, gaat de lijn er wel vloeiender uitzien. Bij t=0,5 blijkt de knikker nog maar 25 cm afgelegd te hebben. Bij t=1,5 is de totaal afgelegde afstand 2,25 m en bij t=2,5 is de totale afstand 6,25 m. Hiernaast is het resultaat afgebeeld, dat we krijgen als we deze extra meetpunten gebruiken.

Maar waar zijn nu de oneven getallen van Galileï gebleven? Ze zijn er nog steeds! Dat is gemakkelijk te zien, als we de afgelegde afstand in elke halve seconde niet weergeven in decimale notatie, maar als breuken. We krijgen dan: 1/4, 3/4, 5/4, 7/4, 9/4, 11/4...

Er zijn ook nog steeds knikken te zien, vooral in de eerste seconde. We zouden nog meer meetpunten kunnen gebruiken, maar het wordt wel erg moeilijk om dat met de hand te meten.

En er is nog een probleem: De lijn ziet er vloeiender uit, maar hij bestaat nog steeds uit rechte lijnstukken en knikken. Er zijn nu zelfs nog meer knikken, dan in de eerste grafiek. Ze vallen alleen wat minder op. Je kunt nog verder gaan, door bijvoorbeeld elke kwart seconde een meting te doen enzovoort... Maar het blijven rechte lijnstukjes. En steeds meer knikken!

En dat is nu het probleem, dat Newton heeft opgelost. Hij bedacht een methode om de lijn op te delen in oneindig veel, oneindige kleine stukjes. Ja, dan zijn er ook oneindig veel knikken. En dat is precies de bedoeling! Een lijn met oneindig veel knikken is overal geknikt. Met andere woorden, het is een kromme lijn! En dat klopt ook met de werkelijkheid.

Ik denk, dat oplettende lezers in de grafiek allang de parabool

s = t^2

hebben herkend. Die is niet zo moeilijk te tekenen. Maar het is inderdaad een kromme lijn. Je kunt er op elk punt je liniaal tegenaan leggen om een raaklijn te tekenen. De helling van je raaklijn geeft de snelheid weer van het voorwerp op dat moment. En dat is wat we willen weten.

Maar is dat ook uit te rekenen? Laten we met iets gemakkelijkers beginnen. Hoe rekenen we de gemiddelde afstand over een traject uit? Dat hebben we al eerder gedaan: We noteren hoe laat een auto twee punten, A en B, passeert. De gemiddelde snelheid was dan de afstand tussen de punten A en B gedeeld door het verschil tussen de twee genoteerde tijden. In formulevorm:

$\frac{s_B-s_A}{t_B-t_A}$

Waarin $s_A$ de afstand is tussen het begin van de route tot punt A en $s_B$ de afstand van het begin van de route tot punt B. $t_A$ en $t_B$ stellen de momenten voor dat de auto respectievelijk punt A en punt B passeerde.

Als we de positie s schrijven als een functie $f(t)$ van de tijd, dan gaat dit er zo uit zien:

$\frac{f(t_B)-f(t_A)}{t_B-t_A}$

Om deze formule wat overzichtelijker te maken, gebruiken we een hulpvariabele $h$, die het verschil aangeeft tussen de tijstippen $t_A$ en $t_B$, dus $h=t_B-t_A$. Dan wordt de formule:

$\frac{f(t_A+h)-f(t_A)}{h}$

Als we nu naar onze waarnemingen van de knikker kijken, dan kunnen we eens wat getallen invoeren en kijken of de formule werkt. Na een seconde had de knikker 1 meter afgelegd. dus $t_A=1$ en $s_A=1$ of $f(t_A)=1$. Na twee seconden had de knikker in totaal 1+3=4 meter afgelegd. dus $t_B=2$ en $s_B=4$ of $f(t_B)=4$ en omdat $h=t_B-t_A=2-1=1$ geldt ook $f(t_A+h)=4$!

$\frac{f(t+h)-f(t)}{h}=\frac{f(1+1)-f(1)}{1}=\frac{4-1}{1}=3$

Precies de drie meter, die de knikker in de tweede seconde rolde en dus precies de gemiddelde snelheid in die seconde. Het kan ook met kleinere stapjes. In de derde halve seconde, dus tussen $t_A=1$ en $t_B=1,5$ rolde de knikker van $s_A=1$ naar $s_B=2,25$. Als we dat invullen, krijgen we:

$\frac{f(t+h)-f(t)}{h}=\frac{f(1+0,5)-f(1)}{0,5}=\frac{2,25-1}{0,5}=\frac{1,25}{0,5}=2,5$

Omdat we de vorm van de grafiek allang geraden hebben, hoeven we geen moeizame metingen meer te doen, we kunnen gewoon op elk tijdstip uitrekenen, waar de knikker zich bevindt volgens de formule:

$s=f(t)=t^2$

Zo kunnen we bijvoorbeeld uitrekenen, wat de uitkomst zou zijn bij een meting over de kwart seconde van t=1 tot t=1,25:

$\frac{f(t+h)-f(t)}{h}=\frac{f(1+0,25)-f(1)}{0,25}=\frac{(1+0,25{)}^2-(1{)}^2}{0,25}=\frac{1,5625-1}{0,25}=2,25$

Door steeds kleinere waarden voor h te kiezen, bereken je de gemiddelde snelheid over een steeds kortere periode. Om de snelheid op een bepaald moment te berekenen, zou je een periode met lenge 0 moeten nemen. Dat kan natuurlijk niet. Het zou betekenen, dat niet alleen h gelijk wordt aan nul, maar ook de in die periode afgelegde weg. En door 0 kun je niet delen! En als je dan ook nog eens nul door nul deelt, dan is de uitkomst echt niet te voorspellen. Newton had dat heel goed in de gaten. Maar hij was brutaal en hij dacht: "Laat ik maar eens kijken, hoever ik kan gaan." Hij wilde gaan tot het uiterste en dat noemde hij, als Engelsman "the limit". Hij schreef dat op in deze vorm:

$\underset{h\to 0}{\lim }\frac{f(t+h)-f(t)}{h}$

Je spreekt dat uit als "De limiet voor h nadert to nul van..." ...van dat wat er achter staat. Als we onze functie $s=f(t)=t^2$ als voorbeeld nemen, dan kunnen we proberen om dit uit te rekenen:

$\underset{h\to 0}{\lim }\frac{f(t+h)-f(t)}{h}=\underset{h\to 0}{\lim }\frac{(t+h{)}^2-t^2}{h}=\underset{h\to 0}{\lim }\frac{t^2+2th+h^2-t^2}{h}=...$

Boven de deelstreep kunnen we $t^2$ en $-t^2$ tegen elkaar wegstrepen:

$\underset{h\to 0}{\lim }\frac{f(t+h)-f(t)}{h}=\underset{h\to 0}{\lim }\frac{2th+h^2}{h}=...$

Verder zien de boven en onder de deelstreep een gemeenschappelijke term $h$, die kunnen we uitdelen, zolang h nog ongelijk aan 0 is:

$\underset{h\to 0}{\lim }\frac{f(t+h)-f(t)}{h}=\underset{h\to 0}{\lim }\frac{2th+h^2}{h}=\underset{h\to 0}{\lim }\frac{2t+h}{1}=...$

Maar nu is er opeens geen probleem meer! We kunnen gewoon de waarde 0 voor h invullen!

$\underset{h\to 0}{\lim }\frac{f(t+h)-f(t)}{h}=\underset{h\to 0}{\lim }\frac{2t+h}{1}=\frac{2t+0}{1}=2t$

Geweldig! We hebben nu de snelheid uitgerekend op elk moment t! We kunnen de snelheid nu dus schrijven als een functie van de tijd

$v=v(t)=2t.$

Wat we hier zojuist gedaan hebben is te danken aan het inzicht van Newton. Newton bedacht deze techniek, die bekend staat als differentiëren. En dat vergrootte niet alleen ons inzicht in vallende lichamen, maar ook ons inzicht in de wiskunde!

Maar we zijn er nog steeds niet! De formule $F=ma$ ging over de versnelling van een voorwerp, niet over de snelheid. We hebben gezien, dat de gemiddelde snelheid van een voorwerp is uit te rekenen als de mate waarin het voorwerp van positie veranderd, gedeeld door de tijd, die het daarover doet. De snelheid op een bepaald moment rekenen we uit, door net te doen, alsof we de gemiddelde snelheid over een oneindig kort traject in een oneindigkorte tijd kunnen uitrekenen.

Nu is het nog maar een kleine stap van snelheid naar versnelling. De kunnen de gemiddelde versnelling definieren als de mate waarin een voorwerp van snelheid veranderd, gedeeld door de tijd die het daar over doet. In formule:

$\frac{v_B-v_A}{t_B-t_A}$

Waarin $v_A$ de snelheid is op punt A en $v_B$ de snelheid op punt B. $t_A$ en $t_B$ stellen weer de momenten voor dat het voorwerp respectievelijk punt A en punt B passeerde.

Dat lijkt ontzettend veel op de formule, die we vonden voor de gemiddelde snelheid. Natuurlijk willen we ook nu de versnelling op elk tijdstip weten, we zijn niet tevreden met een gemiddelde versnelling.

Daarom gaan we dezelfde truc opnieuw toepassen. We schrijven de snelheid als functie van de tijd: $v=v(t)$. We hadden al uitgerekend, dat voor de knikker geldt: $v(t)=2t$. Om de versnelling op elk moment te bepalen, gaan we weer differentieren:

$a=\underset{h\to 0}{\lim }\frac{v(t+h)-v(t)}{h}=\underset{h\to 0}{\lim }\frac{2(t+h)-2t}{h}=\underset{h\to 0}{\lim }\frac{2t+2h-2t}{h}=\underset{h\to 0}{\lim }\frac{2h}{h}=\underset{h\to 0}{\lim }\frac{2}{1}=2$

Ja! Er komt gewoon 2 uit. De versnelling van deze knikker is overal hetzelfde. Vandaar, dat hij steeds harder gaat! Hij beweegt met een constante versnelling of, zoals natuurkundigen zeggen: "Het is een eenparig versnelde beweging."

Meerdimensionale beweging

Vector

Indien we een twee- of driedimensionale beweging willen voorstellen, hebben we te maken met meer dan een coördinaat. Het is gebruikelijk en overzichtelijk om gebruik te maken van vectoren. Een vector heeft een

• zin
• richting
• grootte
• aangrijpingspunt

Een vector wordt vaak genoteerd als een symbool met een pijltje erboven. Zo stellen we de positie voor door $\overrightarrow{x}$ of $\overrightarrow{r}$, een vector met twee of drie coördinaten.

Positie

We geven de positie van een bewegend punt op het tijdstip t weer door:

$\overrightarrow{x}(t)$

Verplaatsing

Als een punt beweegt van de positie $\overrightarrow{x}(t_1)={\overrightarrow{x}}_1$ op het tijdstip $t_1$ naar de positie $\overrightarrow{x}(t_2)={\overrightarrow{x}}_2$ op het tijdstip $t_2$, is de verplaatsing:

$\mathrm{\Delta }\overrightarrow{x}={\overrightarrow{x}}_2-{\overrightarrow{x}}_1$

Gemiddelde snelheid

De tijd die nodig was voor de bovengenoemde verplaatsing bedraagt

$\mathrm{\Delta }t=t_2-t_1$,

zodat voor de gemiddelde snelheid gedurende deze verplaatsing geldt:

${\overrightarrow{v}}_{gem}=\frac{{\overrightarrow{x}}_2-{\overrightarrow{x}}_1}{t_2-t_1}=\frac{\mathrm{\Delta }\overrightarrow{x}}{\mathrm{\Delta }t}$

Momentane snelheid

We willen ook graag weten wat de (momentane) snelheid op een bepaald tijdstip is. We proberen dat te weten te komen door het tijdsinterval Δt steeds kleiner te nemen en wel door $t_2$ steeds dichter bij $t_1$ te nemen. In de limiet, voor Δt naar 0, krijgen we:

$\overrightarrow{v}(t_1)=\underset{t_2\to t_1}{\lim }\frac{{\overrightarrow{x}}_2-{\overrightarrow{x}}_1}{t_2-t_1}$.

Algemeen vinden we voor de snelheid op het tijdstip t:

$\overrightarrow{v}(t)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }\overrightarrow{x}}{\mathrm{\Delta }t}=\frac{d\overrightarrow{x}}{dt}$.

Versnelling

Als gedurende een beweging de snelheid verandert, spreken we van versnelling. Versnelling kan bijvoorbeeld inhouden dat een voorwerp sneller of langzamer gaat bewegen of van richting verandert. Als de snelheid op het tijdstip $t_1$ gelijk is aan $\overrightarrow{v}(t_1)={\overrightarrow{v}}_1$ en op het tijdstip $t_2$ gelijk aan $\overrightarrow{v}(t_2)={\overrightarrow{v}}_2$, is de gemiddelde versnelling in dat tijdsinterval:

${\overrightarrow{a}}_{gem}=\frac{{\overrightarrow{v}}_2-{\overrightarrow{v}}_1}{t_2-t_1}=\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}$

Ook hier vinden we de momentane versnelling op het tijdstip t door het tijdsinterval Δt naar 0 te laten gaan:

$\overrightarrow{a}(t)=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }\overrightarrow{v}}{\mathrm{\Delta }t}=\frac{d\overrightarrow{v}}{dt}=\frac{d^2\overrightarrow{x}}{d{t}^2}$.

De eenparige cirkelvormige beweging

Een belangrijk voorbeeld van de tweedimensionale beweging is de eenparige cirkelvormige beweging.

Een voorwerp beweegt op een cirkel met straal r en middelpunt de oorsprong. De hoeksnelheid $\omega$ geeft aan hoe de hoek verandert als functie van de tijd. De beweging is eenparig, zodat in gelijke tijden gelijke hoeken worden doorlopen, wat inhoudt dat de hoeksnelheid $\omega$ constant is. In een tijd $\mathrm{\Delta }t$ beweegt het voorwerp zich over een hoek $\mathrm{\Delta }\theta =\omega \mathrm{\Delta }t$. Voor de positie $\overrightarrow{x}(t)$ geldt:

$|\overrightarrow{x}(t)|=r$

en in een rechthoekig assenkruis:

$x_1(t)=r\cos (\omega t)$

en

$x_2(t)=r\sin (\omega t)$,

waarbij we er van uitgegaan zijn dat de beweging in het punt (1,0) is begonnen. We kunnen de beweging dus ook beschrijven door:

$\overrightarrow{x}(t)=r(\cos (\omega t),\sin (\omega t))$.

Daaruit vinden we de snelheid als:

$\overrightarrow{v}(t)=\frac{d\overrightarrow{x}}{dt}=\frac{d}{dt}r(\cos (\omega t),\sin (\omega t))=r\omega (-\sin (\omega t),\cos (\omega t))$.

Dit is een vector met constante grootte

$|\overrightarrow{v}(t)|=r\omega$

en richting volgens

$(-\sin (\omega t),\cos (\omega t))$,

dus loodrecht op $\overrightarrow{x}(t)$, en dus rakend aan de cirkel.

Voor de versnelling leiden we af:

$\overrightarrow{a}(t)=\frac{d\overrightarrow{v}}{dt}=\frac{d}{dt}r\omega (-\sin (\omega t),\cos (\omega t))=-r{\omega }^2(\cos (\omega t),\sin (\omega t))=-{\omega }^2\overrightarrow{x}(t)$.

De versnelling is dus een vector met constante grootte:

$|\overrightarrow{a}(t)|={\omega }^{2}r$

en richting volgens $-\overrightarrow{x}(t)$, dus naar het middelpunt van de cirkel gericht en daarom centripetale (middelpuntzoekende) versnelling geheten.

De afstand waarover bewogen wordt in een tijdsinterval Δt is rωΔt, de snelheid is dus:

$v=\frac{\omega r\mathrm{\Delta }t}{\mathrm{\Delta }t}=\omega r$

Dit is de grootte van de snelheid. De snelheid is een vector, met grootte $\omega .r$ en als richting de raaklijn aan de cirkel. De grootte van de snelheid is constant maar de richting verandert voortdurend, dus de massa wordt versneld.

Op dezelfde manier als hierboven kunnen we aantonen dat de grootte van de normale versnelling gelijk is aan:

$a=\omega v={\omega }^{2}r=\frac{v^2}{r}$.

De versnelling is naar binnen gericht, naar het middelpunt, langs de straal van de cirkel. Dit is de centripetale versnelling. Deze versnelling kunnen we als vector schrijven als:

$\overrightarrow{a}=-{\omega }^2\overrightarrow{r}=-\frac{v^2}{r^2}\overrightarrow{r}$