Sterkteleer/Basisbegrippen

Het begrip Spanning

Bij de invoering van het begrip snede en de snedekrachten werden alle krachten inwerkend op de snede herleid tot een resultante en een moment. De resultante en het moment werden door projectie in een assenkruis omgevormd tot een normaalkracht, dwarskracht, buigmoment en wringmoment op de snede. Al deze krachten werken in op het zwaartepunt van de snede. Door toepassing van de evenwichtsvergelijkingen uit de statica, kan men in elke snede de snedekrachten bepalen.

De tot hiertoe gebruikte technieken en rekenmethodes, volstaan echter niet om de interne krachtswerking in een bepaald punt van een snede te kennen. Hiertoe voeren we het begrip spanning in.

De resultante $\overrightarrow{F}$ en het moment op een snede is niet 1 kracht die inwerkt op het zwaartepunt, maar kunnen we beschouwen als de vectorsom van alle deelkrachten $\overrightarrow{\mathrm{\Delta }F}$ die inwerken op diverse deeloppervlakjes $\mathrm{\Delta }S$ van de snede $S$.

De verhouding van de kracht die op een oppervlakje inwerkt tot dit oppervlakje kunnen we noteren als $\frac{\overrightarrow{\mathrm{\Delta }F}}{\mathrm{\Delta }S}$

We definiëren de spanningsvector $\overrightarrow{t}$ als de verhouding $\frac{\overrightarrow{\mathrm{\Delta }F}}{\mathrm{\Delta }S}$ waarbij de beschouwde oppervlakte zo klein wordt dat deze kan beschouwd worden als een punt in de snede S. Wiskundig uitgedrukt geeft dit:

Deze spanningsvector heeft als dimensie [kracht per oppervlakte] of als eenheid N/m² (Newton per vierkante meter).

De spanningsvector $\overrightarrow{t}$ kunnen we ontbinden in een component gelegen loodrecht op het oppervlak $\mathrm{\Delta }S$ en een component gelegen in het vlak van $\mathrm{\Delta }S$:

• De component loodrecht op $\mathrm{\Delta }S$ noemen we de normaalspanning en duiden we aan als $\sigma$.
• De component in het vlak van $\mathrm{\Delta }S$ noemen we de schuifspanning en duiden we aan als $\tau$.

Ruimtelijke spanningstoestand

Spanningen in een willekeurig punt van een continu lichaam

In een "punt P" van een lichaam kunnen we oneindig veel vlakjes beschouwen en op elk van deze vlakjes kunnen we de normaalspanning $\sigma$ bepalen die loodrecht op het gekozen vlakje inwerkt en de schuifspanning $\tau$ die evenwijdig aan het gekozen vlakje inwerkt. Gezien het telkens om spanningen gaat die op het zelfde "punt P" inwerken, bekijken we welk verband er bestaat tussen de spanningen in een punt op vlakjes met diverse oriëntaties.

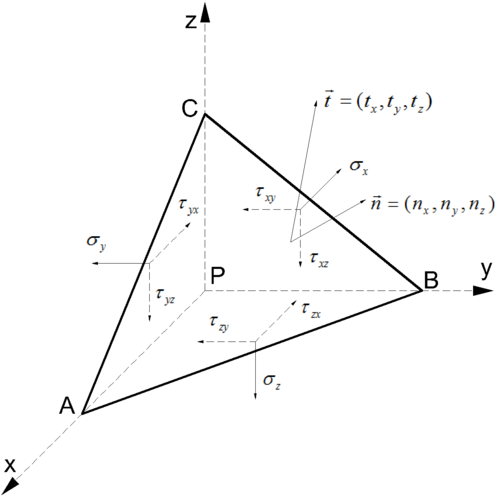
We beschouwen het punt P in een lichaam. Een punt dient niet geïnterpreteerd te worden zoals in de meetkunde, maar eerder als een oneindig klein materieeldeeltje waarop krachten en spanning kunnen inwerken. We plaatsen in dit punt P een rechthoekig assenkruis en een willekeurig vlakje ABC, dat "oneindig" dicht bij het punt het P ligt. Op dit vlakje ABC werkt de spanningsvector $\overrightarrow{t}=(t_x,t_y,t_z)$. De eenheidsvector loodrecht op het vlak ABC wordt aangeduid met $\overrightarrow{n}=(n_x,n_y,n_z)$. De eenheidsvectoren volgens de x-as, y-as en z-as zijn respectievelijk ${\overrightarrow{e}}_x=(1,0,0)$, ${\overrightarrow{e}}_y=(0,1,0)$ en ${\overrightarrow{e}}_z=(0,0,1)$. De oppervlakte van de driehoek ABC noemen we S.

Sjabloon:Clearleft

De vector n kan ontbonden volgens de basisvectoren:

$\overrightarrow{n}=n_x.{\overrightarrow{e}}_x+n_y.{\overrightarrow{e}}_y+n_z.{\overrightarrow{e}}_z$

We kunnen de oppervlakte van de volgende driehoeken schrijven als volgt:

oppervlakte PBC = $S_{PBC}=S\overrightarrow{n}.{\overrightarrow{e}}_x=S.n_x$

oppervlakte PCA = $S_{PCA}=S\overrightarrow{n}.{\overrightarrow{e}}_y=S.n_y$

oppervlakte PAB = $S_{PAB}=S\overrightarrow{n}.{\overrightarrow{e}}_z=S.n_z$

We kunnen voor het elementair deeltje PACB ook het krachtenevenwicht uitschrijven:

$S.\overrightarrow{t}.\overrightarrow{e_x}=S.t_x=S_{PBC}.{\sigma }_x+S_{PCA}.{\tau }_{yx}+S_{PAB}.{\tau }_{zx}$

$S.\overrightarrow{t}.\overrightarrow{e_y}=S.t_y=S_{PBC}.{\tau }_{xy}+S_{PCA}.{\sigma }_y+S_{PAB}.{\tau }_{zy}$

$S.\overrightarrow{t}.\overrightarrow{e_z}=S.t_z=S_{PBC}.{\tau }_{xz}+S_{PCA}.{\tau }_{yz}+S_{PAB}.{\sigma }_z$

Deling door de oppervlakte S levert:

$t_x=n_x.{\sigma }_x+n_y.{\tau }_{yx}+n_z.{\tau }_{zx}$

$t_y=n_x.{\tau }_{xy}+n_y.{\sigma }_y+n_z.{\tau }_{zy}$

$t_z=n_x.{\tau }_{xz}+n_y.{\tau }_{yz}+n_z.{\sigma }_z$

Dit levert vectorieel de formule op Sjabloon:Formulenum waarbij:

• $\overrightarrow{t}$  : De spanningsvector op een vlak met willekeurige oriëntatie.
• $\overrightarrow{n}$  : De eenheidsvector loodrecht op ditzelfde vlak.
• $T_s=\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z\end{array}\right]$  : Deze matrix wordt de spanningstensor genoemd.

Deze laatste vergelijkingen betekenen dat op een vlakje met willekeurige oriëntatie door het punt P, bepaald door de eenheidsvector n loodrecht op dit vlakje, de spanningscomponenten op dit vlakje gekend zijn als de 9 componenten van de spanningstensor T_s gekend zijn.

In de spanningstensor worden de 9 componenten als volgt aangeduid:

• ${\sigma }_x,{\sigma }_y,{\sigma }_z$ = normaalspanning volgens respectievelijk de x-as, de y-as en de z-as. Trekspanningen zijn positief.
• ${\tau }_{yx},{\tau }_{zx},{\tau }_{xy},{\tau }_{zy},{\tau }_{xz},{\tau }_{yz}$ = schuifspanningen. De eerste index is deze van de as die loodrecht staat op het werkingsvlak van de schuifspanning, de tweede index is deze van de as volgens dewelke $\tau$ gericht is. De positieve zin van de schuifspanningen wordt genomen volgens de positieve asrichtingen.

Symmetrie van de spanningstensor

Nu aangetoond is dat we spanningen op een willekeurig vlak door een punt kunnen bepalen als de spanningen op drie onderling loodrechte vlakjes en dus de spanningstensor gekend is, kunnen we ons verder beperken tot een kubisch lichaam.

Sjabloon:Clearleft

We beschouwen een elementair elementje met lengte dx, breedte dy en hoogte dz zoals op de tekening hierboven.
Op het linkse vlakje, het achterste vlakje en het onderste vlakje werken de spanningscomponenten ${\sigma }_x,{\sigma }_y,{\sigma }_z,{\tau }_{yx},{\tau }_{zx},{\tau }_{xy},{\tau }_{zy},{\tau }_{xz},{\tau }_{yz}$. Deze 9 spanningscomponten vormen de spanningstensor. Op het voorste, bovenste en rechtse vlakje zijn deze spanningscomponten aangegroeid tot ${\sigma }_x+d{\sigma }_x,{\sigma }_y+d{\sigma }_y,{\sigma }_z+d{\sigma }_z,{\tau }_{yx}+d{\tau }_{yx},{\tau }_{zx}+d{\tau }_{zx},{\tau }_{xy}+d{\tau }_{xy},{\tau }_{zy}+d{\tau }_{zy},{\tau }_{xz}+d{\tau }_{xz},{\tau }_{yz}+d{\tau }_{yz}$.
In het zwaartepunt van de het element werkt een kracht F in met componten (X,Y,Z).

Het evenwicht van dit elementje wordt uitgedrukt door de 6 evenwichtwichtsvergelijkingen. Indien we het evenwicht uitschrijven van het rotatie-evenwicht rond een as door het zwaartepunt evnwijdig aan de z-as krijgen we volgende uitdrukking:

$-({\tau }_{yx}.dx.dz)\frac{dy}{2}-({\tau }_{yx}+d{\tau }_{yx}).dx.dz\frac{dy}{2}+({\tau }_{xy}.dy.dz)\frac{dx}{2}+({\tau }_{xy}+d{\tau }_{xy}).dy.dz\frac{dx}{2}=0$

Na vereenvoudiging en deling door dx.dy.dz geeft dit:

$-{\tau }_{yx}+{\tau }_{xy}-\frac{d{\tau }_{yx}}{2}+\frac{d{\tau }_{xy}}{2}=0$

Met verwaarlozing van de tweede orde termen geeft dit:

$-{\tau }_{yx}+{\tau }_{xy}=0$

Het rotatie-evenwicht rond de x-as en y-as levert analoge betrekkingen zodat we kunnen stellen dat:

Reprociteitsbeginsel
${\tau }_{yz}={\tau }_{zy}$   ${\tau }_{zx}={\tau }_{xz}$ ${\tau }_{yx}={\tau }_{xy}$

De spanningstensor T_s is bijgevolg een symmetrische matrix. Men noemt dit "het beginsel van de wederkerigheid van de schuifspanningen" of het "reprociteitsbeginsel".

Benaming specifieke spanningstoestanden

Bij vele problemen zijn niet alle spanningscomponten van de spanningstensor T_s verschillend van nul. Enkele specifieke gevallen worden apart aangeduid:

Vlakke spanningstoestand

De vlakke spanningstoestand is de toestand waarbij alle vlakjes evenwijdig aan één bepaald vlak spanningsloos zijn. Als dit vlak bijvoorbeeld het xy-vlak is geldt:

	${\sigma }_z=0$
	${\tau }_{zx}={\tau }_{xz}={\tau }_{zy}={\tau }_{yz}=0$

Aangezien op de vlakjes evenwijdig aan het xy-vlak geen spanningen werken kan deze spanningstoestand in een 2-dimesionaal assenkruis worden getekend. een vlakke spanningstoestand treedt bijvoorbeeld op bij in hun vlak belaste wanden.

Lijnspanningstoestand

Een nog eenvoudigere toestand is de lijnspanning. Deze treedt op als alle vlakjes evenwijdig aan één bepaalde lijn spanningloos zijn. Is deze lijn gelijk aan de x-as dan is enkel ${\sigma }_x$ verschillend van 0. Het typische geval van een lijnspanningstoestand is een centrisch belaste staaf.

Evenwichtsvergelijkingen in functie van spanning

Uit de drie rotatie-evenwichten van een elementair belast elementje, werd hoger het reprociteitsbeginsel afgeleid. De krachten die op het elementje inwerken moeten ook voldoen aan het translatie-evenwicht. De krachten X, Y en Z beschouwen we als volumekrachten met dimensie [Kracht per volume] en als grootheid [N/m³].

Sjabloon:Clearleft

Het translatie-evenwicht volgens de x-as geeft hetvolgende:

$({\sigma }_x+d{\sigma }_x).dy.dz-{\sigma }_x.dy.dz+({\tau }_{yx}+d{\tau }_{yx}).dx.dz-{\tau }_{yx}.dx.dz+({\tau }_{zx}+d{\tau }_{zx}).dx.dy-{\tau }_{zx}.dx.dy+X.dx.dy.dz=0$

Door ontwikkeling van ${\sigma }_x+d{\sigma }_x$, ${\tau }_{xy}+d{\tau }_{xy}$ en ${\tau }_{zx}+d{\tau }_{zx}$ in een Taylorreeks en de hogere-orde termen te verwaarlozen vinden we:

$d{\sigma }_x=\frac{\partial {\sigma }_x}{\partial x}.dx$ en $d{\tau }_{yx}=\frac{\partial {\tau }_{yx}}{\partial y}.dy$ en $d{\tau }_{zx}=\frac{\partial {\tau }_{zx}}{\partial z}.dz$

Ingevuld en na eneige vereenvoudigingen geeft dit:

$\frac{\partial {\sigma }_x}{\partial x}.dx.dy.dz+\frac{\partial {\tau }_{yx}}{\partial y}.dx.dy.dz+\frac{\partial {\tau }_{zx}}{\partial z}.dx.dy.dz+X.dx.dy.dz=0$

Deling door het volume dx.dy.dz en analoge afeleidingen voor het evenwicht volgens de y-as en de z-as leveren uiteindelijk de drie evenwichtsvergelijkingen op in functie van de spanning:

Evenwichtsvergelijkingen in functie van spanning
$\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}+X=0$ $\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+Y=0$ $\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_z}{\partial z}+Z=0$

In elk punt van een lichaam moeten de spanningen aan deze bovenstaande vergelijkingen voldoen.

Aan de rand van een lichaam moeten de spanningen echter ook in evenwicht zijn met de uitwendige krachten die op het oppervlak werken. Als $\bar{X}$, $\bar{Y}$ en $\bar{Z}$ de componenten zijn van de uitwendige belasting per eenheid van oppervlakte in een randpunt van een lichaam, dan moeten de spanningen in dit randpunt voldoen aan de Sjabloon:Formuleref die hoger zijn afgeleid voor de spanningen in een punt, waaruit volgt:

Randvoorwaarden bij de evenwichtsvergelijkingen in functie van spanning
$\bar{X}=n_x.{\sigma }_x+n_y.{\tau }_{yx}+n_z.{\tau }_{zx}$ $\bar{Y}=n_x.{\tau }_{xy}+n_y.{\sigma }_y+n_z.{\tau }_{zy}$ $\bar{Z}=n_x.{\tau }_{xz}+n_y.{\tau }_{yz}+n_z.{\sigma }_z$ met $\overrightarrow{n}=(n_x,n_y,n_z)$ de naar buiten gerichte eenheidsvector loodrecht op het oppervlak in het beschouwde randpunt

Deze laatste vergelijkingen noemt men de randvoorwaarden van de evenwichtsvergelijkingen.

In een aan externe krachten onderworpen lichaam, moeten de spanningen voldoen aan de drie evenwichtsvergelijingen en aan de randvoorwaarden.

In de meeste gevallen zullen de drie evenwichtsvergelijkingen niet volstaan om de 6 spanningscomponten te bepalen en moeten de (elastische) vervormingen van het lichaam in rekening gebracht worden.

Ruimtelijke vervormingstoestand

Verplaatsingen als functies

Een lichaam waarop krachten inwerken, ondergaat vervormingen. In de figuur hieronder zien we twee eenvoudige voorbeelden. In de figuur links is de verlenging van een staaf geschetst, belast door een trekkracht P. Voor elke snede x heeft de verplaatsing u(x) een andere waarde. De figuur rechts toont de doorbuiging van een balk op twee steunpunten onder invloed van een puntlast p. De vertikale verplaatsing kan in elke snede x uitgedrukt worden als v(x). Sjabloon:Clearleft We kunnen de verplaatsingen en vormveranderingen van een lichaam bepalen door in elk punt (x,y,z) van dit lichaam de verplaatsingencomponenten u, v en w te bepalen:

• u(x,y,z)= de verplaating van een punt volgens de x-as
• v(x,y,z)= de verplaating van een punt volgens de y-as
• w(x,y,z)= de verplaating van een punt volgens de z-as

De samenhang van het lichaam mag bij de elastische vormverandering niet verbroken worden (het materiaal mag niet scheuren), zodat u, v en w continue functies moeten zijn van de plaatscoördinatoren x, y en z.

We beschouwen twee oneindig dicht bij elkaar gelegen punten P=(x,y,z) en Q=(x+dx,y+dy,z+dz) zoals op figuur hieronder. De punten P en Q ondergaan een verplaatsing naar de punten P1 en Q1. De verplaatsingen van deze punten zullen slechts een elementaire toename van mekaar mogen verschillen. u(x,y,z), v(x,y,z) en w(x,y,z) zijn de verplaatsingscomponten in P en u+du, v+dv en w+dw zijn de verplaatsingscomponten in Q. Sjabloon:Clearleft We kunnen de verplaatsingcomponten benaderen door de deze te ontwikkelen in een taylorreeks rond (x,y,z):

u+du = u(x+dx, y+dy, z+dz)

$u+du=u(x,y,z)+\frac{\partial u}{\partial x}.\frac{dx}{1!}+\frac{{\partial }^{2}u}{\partial x^2}.\frac{d{x}^2}{2!}+...+\frac{\partial u}{\partial y}.\frac{dy}{1!}+\frac{{\partial }^{2}u}{\partial y^2}.\frac{d{y}^2}{2!}+...+\frac{\partial u}{\partial z}.\frac{dz}{1!}+\frac{{\partial }^{2}u}{\partial z^2}.\frac{d{z}^2}{2!}+...$

Voor v+dv en w+dw kunnen analoge uitdrukkingen neergeschreven worden. Indien we enkel de lineaire termen beschouwen vinden we:

$du=\frac{\partial u}{\partial x}.dx+\frac{\partial u}{\partial y}.dy+\frac{\partial u}{\partial z}.dz$

$dv=\frac{\partial v}{\partial x}.dx+\frac{\partial v}{\partial y}.dy+\frac{\partial v}{\partial z}.dz$

$dw=\frac{\partial w}{\partial x}.dx+\frac{\partial w}{\partial y}.dy+\frac{\partial w}{\partial z}.dz$

Bovenstaande uitdrukkingen zijn geldig wanneer de verplaatsingen zeer klein zijn. Hieraan is voldoaan als we de beschouwde omgeving rond P maar klein genoeg nemen. Een dergelijke vervormingstoestand, waarin de verplaatsingen lineaire functies zijn van de begincoördinaten, wordt homogeen genoemd.

De begrippen Rek en Glijding

Bij een vormverandering van een lichaam veranderen de afstanden tussen twee punten. Ook de hoeken tussen twee rechte lijnen verandert. Om een analyse van de spannings-vervormingstoestand in elastische lichamen mogelijk te maken is een nauwkeurige beschrijving van deze fenomenen nodig.

We beschouwen de punten P en Q uit hogerstaande figuur. Hun onderlinge afstand bedraagt:

$\overline{PQ}=ds=\sqrt{d{x}^2+d{y}^2+d{z}^2}$

Na de vormverandering bedraagt de afstand tussen P1 en Q1:

$\overline{P_1{Q}_1}=d{s}_1=\sqrt{(dx+du{)}^2+(dy+dv{)}^2+(dz+dw{)}^2}$

We vullen de hoger gevonden uitdrukkkingen voor du, dv en dw in deze laatste uitdrukking. Na enig rekenwerk bekomt men:

$d{s}_1=\sqrt{(1+2{\epsilon }_x)d{x}^2+(1+2{\epsilon }_y)d{y}^2+(1+2{\epsilon }_z)d{z}^2+2{\gamma }_{xy}.dx.dy+2{\gamma }_{yz}.dy.dz+2{\gamma }_{zx}.dz.dx}$

In deze laatste formules wordt volgende verkorte notaties gebruikt:

${\epsilon }_x=\frac{\partial u}{\partial x}+\frac{1}{2}[(\frac{\partial u}{\partial x}{)}^2+(\frac{\partial v}{\partial x}{)}^2+(\frac{\partial w}{\partial x}{)}^2]$

${\epsilon }_y=\frac{\partial v}{\partial y}+\frac{1}{2}[(\frac{\partial u}{\partial y}{)}^2+(\frac{\partial v}{\partial y}{)}^2+(\frac{\partial w}{\partial y}{)}^2]$

${\epsilon }_z=\frac{\partial w}{\partial z}+\frac{1}{2}[(\frac{\partial u}{\partial z}{)}^2+(\frac{\partial v}{\partial z}{)}^2+(\frac{\partial w}{\partial z}{)}^2]$

${\gamma }_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}+\frac{\partial u}{\partial x}.\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}.\frac{\partial v}{\partial y}+\frac{\partial w}{\partial x}.\frac{\partial w}{\partial y}$

${\gamma }_{yz}=\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}+\frac{\partial u}{\partial y}.\frac{\partial u}{\partial z}+\frac{\partial v}{\partial y}.\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}.\frac{\partial w}{\partial z}$

${\gamma }_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}+\frac{\partial u}{\partial z}.\frac{\partial u}{\partial x}+\frac{\partial v}{\partial z}.\frac{\partial v}{\partial x}+\frac{\partial w}{\partial z}.\frac{\partial w}{\partial x}$

Deze grootheden ε en γ hebben een belangrijke fysische betekenis en nomen we respectievelijk rek en glijding. In het verder verloop van de afleidingen wordt steeds aangenomen dat de vervormingen dermate klein zijn, zodat in bovenstaande uitdrukkingen de kwadraten en producten van de afgeleiden verwaarloosbaar zijn tegenover de lineaire termen. Deze uitdrukkingen kunnen dan vereenvoudigd worden tot de zogenaamde geometrische betrekkingen tussen de rek/glijding en de verplaatsingen:

Geometrische betrekkingen tussen vervormingen en verplaatsingen
${\epsilon }_x=\frac{\partial u}{\partial x}$ ${\epsilon }_y=\frac{\partial v}{\partial y}$ ${\epsilon }_z=\frac{\partial w}{\partial z}$ ${\gamma }_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}$ ${\gamma }_{yz}=\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}$ ${\gamma }_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}$

Uit bovenstaande uitdrukkingen blijkt ook dat rekken en glijdingen geen "willekeurige" functies zijn van de plaatscoördinatoren x, y en z maar dat ze onderling verbonden zijn via de verplaatsingfuncties u, v en w.

Fysische betekenis van rek en glijding

Sjabloon:Clearleft

We beschouwen op de bovenstaande figuur de punten P(x,y,z), Q(x+dx,y,z) en R(x,y+dy,z), die verplaatsingen ondergaan naar P1, Q1 en R1.

Rek

Het lijnstuk PQ is gelegen evenwijdig aan de x-as. De originele lengte van het lijnstuk voor vervorming is gelijk aan dx. De lengte van dit lijnstuk na de vormververandering wordt gegeven door de formule uit de vorige paragraaf waarbij dy=dz=0 :

$\overline{P_1{Q}_1}=d{s}_1=\sqrt{(1+2{\epsilon }_x).d{x}^2}=dx\sqrt{(1+2{\epsilon }_x)}\approx dx.(1+{\epsilon }_x)$

Gezien ε_x zeer klein verondersteld wordt, kunnen we $\sqrt{(1+2{\epsilon }_x)}$ benaderen door 1+ε_x, door ontwikkeling van $\sqrt{(1+2{\epsilon }_x)}$ in een taylorreeks en enkel de lineaire term te behouden.
Wanneer we de verlenging van het lijnstuk PQ beschouwen, krijgen we volgende uitdrukking:

$\overline{P_1{Q}_1}-\overline{PQ}=d{s}_1-dx=dx.(1+{\epsilon }_x)-dx={\epsilon }_x.dx$

$=>{\epsilon }_x=\frac{d{s}_1-dx}{dx}=\frac{\mathrm{\Delta }L}{L}$

Deze uitdrukking betekent dat de rek ${\epsilon }_x$ gelijk is aan de verhouding tussen de verlenging en de oorspronkelijke lengte (of kortweg de relatieve verlenging) van een lijnstuk evenwijdig aan de x-as. Op een analoge manier kunnen we vinden dat de rekken ${\epsilon }_y$ en ${\epsilon }_z$ de relatieve verlengingen zijn volgens de y-as en de z-as.

Glijding

We kunnen ook de hoek ${\phi }_{xy}$ berekenen. Deze hoek is de vervormde hoek tussen de lijnstukken P1Q1 en P1R1. PQ en PR staan loodrecht op elkaar. Er geldt:

$\overline{P_1{Q}_1}=dx\sqrt{(1+2{\epsilon }_x)}$

$\overline{P_1{R}_1}=dy\sqrt{(1+2{\epsilon }_y)}$

We passen nu de cosinusregel toe op de driehoek P1Q1R1 :

$\stackrel{2}{\stackrel{‾}{Q_1{R}_1}}=\stackrel{2}{\stackrel{‾}{P_1{Q}_1}}+\stackrel{2}{\stackrel{‾}{P_1{R}_1}}-2.\overline{P_1{Q}_1}.\overline{P_1{R}_1}.\cos {\phi }_{xy}$

$\stackrel{2}{\stackrel{‾}{Q_1{R}_1}}=(1+2{\epsilon }_x).d{x}^2+(1+2{\epsilon }_y).d{y}^2-2.dx.dy.\sqrt{(1+2{\epsilon }_x)(1+2{\epsilon }_y)}.\cos {\phi }_{xy}$

We kunnen de afstand Q1R1 ook berekenen met de formule uit de vorige paragraaf, waarbij dz=0, en dx van Q naar R negatief.

$\overline{Q_1{R}_1}=\sqrt{(1+2{\epsilon }_x)(-dx{)}^2+(1+2{\epsilon }_y)d{y}^2+2{\gamma }_{xy}.(-dx).dy}$

$\stackrel{2}{\stackrel{‾}{Q_1{R}_1}}=(1+2{\epsilon }_x).d{x}^2+(1+2{\epsilon }_y).d{y}^2-2{\gamma }_{xy}.dx.dy$

Gelijk stellen van de twee berekeningswijzes voor de afstand levert:

$\cos {\phi }_{xy}=\frac{{\gamma }_{xy}}{\sqrt{(1+2{\epsilon }_x)(1+2{\epsilon }_y)}}\approx {\gamma }_{xy}$

De oorspronkelijke hoek tussen PQ en PR was een rechte hoek of $\frac{\pi }{2}$ in radialen.
De verandering van de hoek bedraagt $\frac{\pi }{2}-{\phi }_{xy}$. Aangezien deze hoek een zeer kleine hoek geldt dat de sinus van deze hoek bij benadering gelijk is aan de hoek zelf in radialen.

${\gamma }_{xy}\approx \cos {\phi }_{xy}=\sin (\frac{\pi }{2}-{\phi }_{xy})\approx \frac{\pi }{2}-{\phi }_{xy}$

$=>{\gamma }_{xy}=\frac{\pi }{2}-{\phi }_{xy}$

We stellen vast dat de glijding ${\gamma }_{xy}$ de verandering van hoek voorstelt tussen twee oorspronkelijk loodrechte lijnstukken in het xy-vlak. Op een analoge manier kan men aantonen dat ${\gamma }_{yz}$ en ${\gamma }_{zx}$ de verandering van een rechte hoek in het yz-vlak en het zx-as voorstellen.

Toepassing: Kubische volumeverandering

Een lichaam dat vervormt zal meestal ook een volumeverandering ondergaan. Aangezien de glijdingen die de hoekverandering bepalen tussen twee oorspronkelijk loodrechte lijnen zeer klein zijn, kunnen we deze glijdingen verwaarlozen voor elementaire volumeveranderingen. We kunnen volstaan met enkel de rekken ε_x, ε_y en ε_z in rekening te brengen voor de volumeverandering van een elementair kubisch deeltje zoals op de afbeelding hieronder.

Sjabloon:Clearleft

Het oorspronkelijk volume V bedraagt:

$V=dx.dy.dz$

Na vervorming zijn de lengtes van de zijden aangegroeid tot (1+ε_x)dx, (1+ε_y)dy en (1+ε_z)dz. De volumetoename ΔV van het elementair deeltje dx dy dz bedraagt:

$\mathrm{\Delta }V=(1+{\epsilon }_x).(1+{\epsilon }_y).(1+{\epsilon }_z).dx.dy.dz-dx.dy.dz$

De relatieve volumeverandering of kubische dilatatie bedraagt:

$\frac{\mathrm{\Delta }V}{V}=1+{\epsilon }_x+{\epsilon }_y+{\epsilon }_z+{\epsilon }_x.{\epsilon }_y+...-1\approx {\epsilon }_x+{\epsilon }_y+{\epsilon }_z$

Mits verwaarlozing van de hogere orde termen (ε wordt als elementair klein beschouwd) wordt de kubische dilatatie, voorgesteld door het symbool "e" gelijk aan:

$e=\frac{\mathrm{\Delta }V}{V}={\epsilon }_x+{\epsilon }_y+{\epsilon }_z$

---

<< Terug naar Bepaling van de snedekrachten / Verder naar Basisbegrippen - Deel 2 >>